S'initier à la cryptographie post-quantique avec l'échange de clés de chiffrement ML-KEM

03/07/2025 · 21 mins de lecture · cybersecurite physique-quantique ordinateur-quantique qubit cryptographie post-quantum-cryptography pqc lattices mlwe kem kyber ml-kem ·

Partager sur:

Traductions

Sommaire

Dans cet article, je vous propose de partir à la découverte du monde merveilleux de la cryptographie post-quantique avec l’algorithme d’échange de clés Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM), aussi connu sous le nom de Kyber et standardisé en août 2024. Le principe est de fournir un moyen d’échanger des clés de chiffrement en étant robuste aux futurs ordinateurs quantiques, théoriquement capables de casser certains algorithmes cryptographiques actuellement utilisés.

Introduction

La cryptographie est omniprésente pour sécuriser nos données. Grâce à elle, on arrive aujourd’hui à garantir des propriétés essentielles sur les données telles que la confidentialité, l’intégrité, l’authenticité et la non-répudiation. Pour ce faire, elle repose sur des problèmes mathématiques difficiles à résoudre pour un attaquant. Cependant, ces propriétés se retrouvent aujourd’hui menacées par l’arrivée future et probable de l’ordinateur quantique. De par l’utilisation de propriétés des lois de la physique quantique, qui apparaissent pour beaucoup comme de la magie (et ils n’ont pas tout à fait tort !), les capacités de calcul sont décuplées par rapport à un ordinateur classique. Les principaux problèmes mathématiques menacés par l’ordinateur quantique sont le problème du logarithme discret et de la factorisation, qui sont utilisés notamment dans l’échange de clés de chiffrement et le chiffrement asymétrique (utilisation d’une clé publique pour chiffrer les données et d’une clé privée pour déchiffrer les données).

Cryptographie, physique quantique : alors on va faire des maths c’est ça ? Juste ce qu’il faut.

Depuis plusieurs années, un processus de standardisation vise à fournir un ensemble d’algorithmes cryptograhiques robustes aux ordinateurs quantiques : on parle de cryptographie post-quantique ou post-quantum cryptography (parfois aussi quantum-safe/proof/resistant cryptography). Parmi ces algorithmes, Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM) permet l’échange de clés de chiffrement. C’est un Key Encapsulation Mechanism (KEM) post-quantique. Nous y reviendrons.

La cryptographie post-quantique fait ainsi peur à beaucoup de monde de par son intitulé, qui pourrait laisser sous-entendre qu’en plus de compétences mathématiques, il est nécessaire de maîtriser des compétences de physique quantique afin de comprendre ce domaine. Au final, on en reste juste à des mathématiques (et c’est déjà ça !).
Bien que l’ordinateur quantique soit à l’état de preuve de concept et qu’il n’ait pas encore été démontré comme capable de casser les algorithmes cryptographiques traditionnels et considérés historiquement robustes, le National Institute of Standards and Technology (NIST) recommande d’éliminer l’utilisation de cryptographie vulnérable à l’ère post-quantique d’ici à 2035, et près d’un tiers du trafic Web utiliserait déjà la cryptographie post-quantique (selon Cloudflare). Vous pouvez d’ailleurs vérifier ici si votre navigateur Web supporte la cryptographie post-quantique.

Avec cet article, je souhaite apporter des réponses aux questions suivantes dont j’ai cherché les réponses ces derniers mois :

Qu’est-ce qu’un ordinateur quantique ?
Pourquoi l’ordinateur quantique menace-t-il la cryptographie actuelle ?
En quoi la cryptographie post-quantique diffère-t-elle de la cryptographie actuelle ?
Comment la cryptographie post-quantique peut-elle se protéger de l’ordinateur quantique ?

Je vous propose d’abord de comprendre ce qu’est l’ordinateur quantique, puis de plonger dans les notions mathématiques qui permettent de comprendre l’algorithme ML-KEM que nous verrons ensuite plus en détails.

L’ère post-quantique

Richard Feynmann, un physicien américain, disait : Si vous croyez comprendre la mécanique quantique, c’est que vous ne la comprenez pas. Ne vous inquiétez pas donc, il est tout à fait attendu de ne pas tout comprendre dans cette section !

Physique quantique

La physique quantique, née au début du XXème sièce, est l’ensemble des théories qui décrivent le comportement de la matière et de l’énergie à une échelle extrêmement réduite, l’échelle subatomique (plus petite que l’atome). C’est la branche de la physique qui étudie l’infiniment petit, par opposition à la physique classique comme par exemple la théorie de la relativité qui décrit l’espace-temps ou la gravitation. Le terme quantique provient du latin “quantum” qui signifie “combien” ou “quelle quantité”, ce qui renvoie au fait qu’à l’échelle du très petit, des “grains” existent en tant que composants de base pour construire la matière, tels des légos.
La physique quantique, dont les lois sont celles de la mécanique quantique, est difficile à appréhender pour notre cerveau, tant les phénomènes sont contre-intuitifs. Voici les principaux :

la quantification : certaines valeurs observées ne peuvent prendre que des valeurs discrètes (un ensemble fini de valeurs) et non continues. L’atome a par exemple un certain nombre de niveaux d’énergie possibles, un peu comme si vous passiez d’un coup de 0 à 50 km/h avec votre voiture, et non de manière continue.
la dualité onde-particule : les concepts d’onde (propagation d’une perturbation dans un milieu) et de particule font partie du même phénomène. Un bon exemple est celui de la lumière composées de photons : à la fois onde et particule.
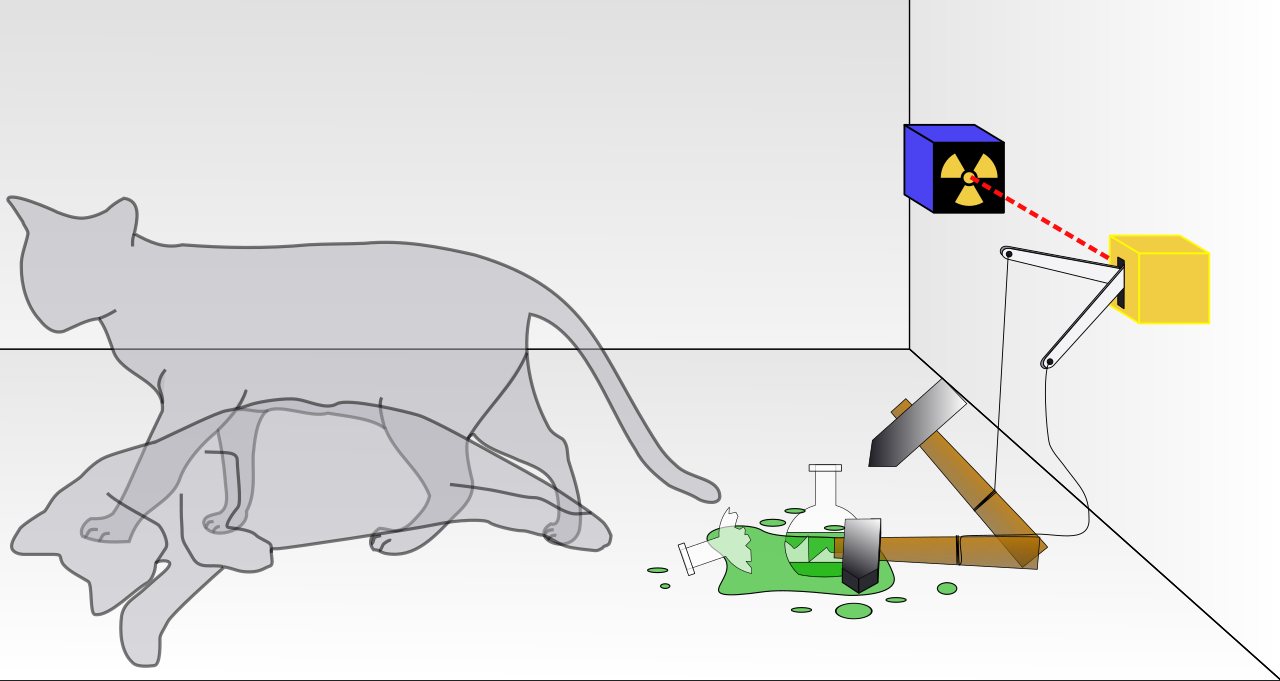
la superposition : une particule peut exister dans plusieurs états ou positions à la fois jusqu’à ce qu’une mesure soit effectuée. C’est l’idée du célèbre “chat de Schrödinger” qui est à la fois mort et vivant. On peut comparer cela à un lancé de pièce de monnaie qui tourne en l’air avant de retomber sur pile ou face : tant que la pièce est en l’air les deux valeurs sont possibles, jusqu’à ce que la pièce retombe et qu’on puisse lire la valeur pile ou face.
l’intrication : l’état d’une particule peut déterminer celui d’une autre, quelle que soit la distance qui les sépare, même des années-lumières (distance que parcourt la lumière en un an), Ceci est totalement contre-intuitif quand on sait qu’Einstein a démontré qu’il existe une vitesse maximale de déplacement de la matière : celle de la lumière.

L'expérience de pensée du chat de Schrödinger qui illustre le principe de superposition : un chat dans une boîte contenant du poison peut être soit vivant soit mort jusqu'à l'ouverture de la boîte délenche le choix (source : https://fr.wikipedia.org/wiki/Chat_de_Schrödinger#/media/Fichier:Schrodingers_cat.svg)

Ordinateur quantique

Les ordinateurs classiques opèrent sur des bits dont la valeur peut être 0 ou 1. Les ordinateurs quantiques opèrent sur des quantum bits ou qubits, dont la valeur peut être 0 et 1 simultanément. Cela est lié à la propriété de superposition quantique que nous venons de voir. Typiquement, on décrit l’état d’un qubit ainsi : $$|\psi\rangle = \alpha|0\rangle + \beta|1\rangle$$ où $\alpha$ et $\beta$ sont des amplitudes de probabilité, qui sont des nombres complexes (extension des nombres réels avec une partie contenant un nombre imaginaire $i$ tel que $i^2 = -1$). L’intégration de nombre complexe amène la notion de phase : sorte d’angle dans l’espace complexe qui décrit l’état du qubit.
La notation de $|\psi\rangle$ signifie qu’on peut observer l’état d’un qubit à 0 avec une probabilité de $|\alpha|^2$ et à 1 avec une probabilité de $|\beta|^2$. Ainsi $|\alpha|^2 + |\beta|^2 = 1$.

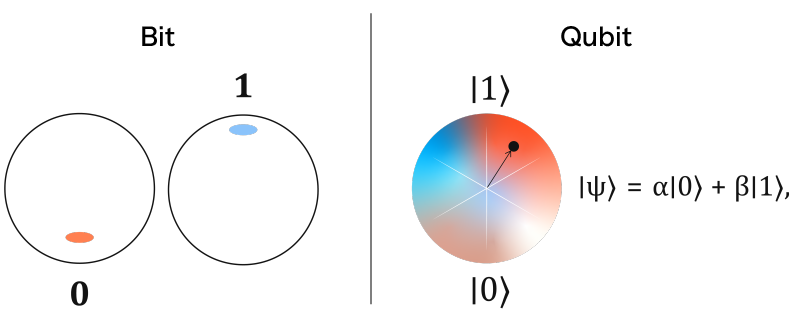
Représentation graphique des états d'un bit classique et d'un qubit à l'aide d'une sphère de Bloch (source : https://www.qnulabs.com/blog/quantum-101-qubit)

Plusieurs qubits peuvent être intriqués, et l’état de 2 qubits représenté comme un état de Bell : $$|\Phi^+\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)$$ Ainsi, la mesure du premier qubit entraîne la même mesure de l’autre qubit.

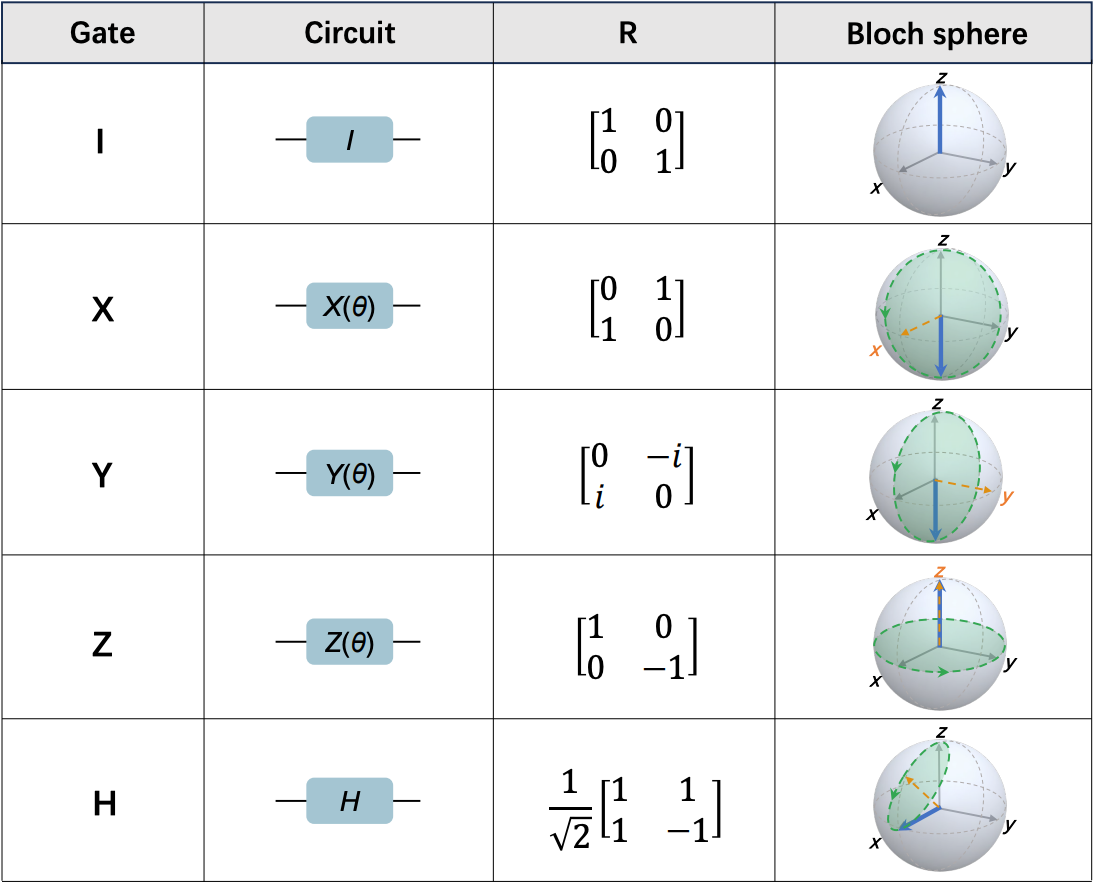
Les opérations sur les qubits au sein d’un ordinateur quantique sont réalisées avec des portes quantiques ou quantum gates. Elles agissent en tant que groupes d’amplitudes, comme une matrice agit lorsqu’elle est multipliée par un vecteur. Les ordinateurs quantiques offrent une meilleure puissance de calcul, car avec $n$ qubit, ils peuvent traiter $2^n$ nombres (l’amplitude des qubits) à la fois et non juste $n$ nombres à la fois comme les ordinateur classiques. Le rôle des portes quantiques est de modifier les amplitudes de probabilité des états superposés. Ces portes peuvent créer et manipuler la superposition, ainsi que créer de l’intrication entre les qubits, ce qui est crucial pour explorer de nombreux chemins de calcul en parallèle. Parmi les multiples portes quantiques, on peut citer quelques exemples :

La porte d’Identité (I) : conserve le qubit dans le même état (pour des tests, de la synchronisation, etc.).
La porte d’Hadamard (H) : permet de créer un état de superposition de deux états sur un qubit permettant le parallélisme dans les calcul.
Les portes de Pauli (X, Y, Z) : l’équivalent des portes logiques classiques (AND, OR, NOT…) permettant le changement d’état (porte X), de phase (porte Z) ou les deux (porte Y).
La porte Controlled-NOT (CNOT ou CX) : permet de créer un état d’intrication pour deux qubits.
La porte Swap (S) : permet d’intervertir deux qubits.

Tableau récapitulatif des portes quantiques I, X, Y, Z et H indiquant la matrice de rotation et la sphère de Bloch qui représente géométriquement l'état d'un qubit avec l'application de la porte quantique (source : Yao, Y.; Xiang, L. Superconducting Quantum Simulation for Many-Body Physics beyond Equilibrium. Entropy 2024, 26, 592. https://doi.org/10.3390/e26070592)

Les algorithmes quantiques sont donc des circuits de portes quantiques qui transforment des amplitudes avant une mesure finale des qubits. C’est ce processus qui permet à l’informatique quantique de résoudre certains problèmes beaucoup plus rapidement que les ordinateurs classiques.
Si je devais vous donner une analogie, l’ordinateur quantique est à la représentation et manipulation de l’information dans un ordinateur ce que le multithreading (parallélisme des instructions informatiques) est au calcul au sein d’un processeur.

Menaces sur la cryptographie

Avec cette nouvelle ère post-quantique, les algorithmes cryptographiques existants sont à risque. En effet, la force de certains problèmes mathématiques réside dans l’impossibilité pour un ordinateur classique de les résoudre. Avec un ordinateur quantique, de nouveaux algorithmes quantiques émergent, et les deux plus célèbres sont Grover et Shor.

L’algorithme de Grover facilite les attaques par force brute en permettant la recherche exhaustive de solutions dans un ensemble d’éléments. Cela permet par exemple de trouver plus facilement une clé de chiffrement Advanced Encryption Standard (AES) de type AES-128 parmi les $2^{128}$ clés possibles en effectuant $2^{64}$ opérations au lieu des $2^{128}$ qu’effectuerait un ordinateur classique. Il est considéré que des clés de longueur supérieure à 200 bits, comme AES-256, offre une résistance aux algorithmes quantiques comme Grover, en garantissant 100 bits de marge de sécurité contre la recherche exhaustive.

L’algorithme de Shor permet de factoriser un grand nombre en nombre premier. Cela est rendu possible grace à la capacité de trouver une période dans une fonction périodique, ce qui permet à l’ordinateur quantique d’évaluer la fonction simultanément pour un très grand nombre de points d’entrée, puis d’utiliser un phénomène d’interférence quantique (similaire à une “onde” qui met en évidence la répétition) pour extraire cette période de manière exponentiellement plus rapide que n’importe quel algorithme classique connu.

Rivest–Shamir–Adleman (RSA, utilisé pour la signature numérique ou l’échange de clés de chiffrement) repose justement sur le problème de la factorisation des grands nombres premiers : trouver $p$ et $q$ nombres premiers en connaissant $N$ tel que $N = p \times q$. L’algorithme Diffie-Hellman (DH) et son application dans les courbes elliptiques en cryptographie ou Elliptic Curve Cryptography (ECC) reposent sur le logarithme discret ou Discrete Logarithm Problem (DLP) qui consiste, si on connaît une valeur $A$, à trouver une valeur $a$ telle que $A = g^a\bmod{p}$ (élever $g$ à la puissance $a$ s’appelle une exponentiation), avec $g$ un nombre donné et $p$ un nombre premier très grand. Or, l’algorithme de Shor a démontré qu’il peut réduire ces problèmes à un problème de recherche de période. Il transforme le problème difficile de factorisation ou logarithme discret en une instance d’un problème de recherche de période dans une fonction spécialement construite.

Il est donc crucial d’anticiper la recherche et standardisation de solution pour remplacer des algorithmes comme RSA, DH ou ECC.

La cryptographie post-quantique

En 2016, le NIST a lancé un appel à candidature ainsi qu’un processus pour standardiser des algorithmes cryptographiques post-quantiques. A l’issue de cela, quatre algorithmes ont été standardisés, dont deux pour les signatures numériques :

Module-Lattice-based Digital Signature Standard (ML-DSA) dérivé de l’algorithme CRYSTALS-Dilithium ;
Stateless Hash-based Digital Signature Standard (SLH-DSA) dérivé de l’algorithme SPHINCS+.

et deux pour l’échange de clé par mécanisme d’encaspulation de clé (KEM) :

Module-Lattice-based Key-Encapsulation Mechanism (ML-KEM) dérivé de l’algorithme Kyber ;
Hamming Quasi-Cyclic (HQC).

La cryptographie post-quantique repose sur plusieurs types d’algorithmes post-quantiques : basé sur les codes (correcteurs d’erreurs), les réseaux euclidiens ou lattices (que nous allons voir juste après), les fonctions de hachage ou bien multivariés (reposant sur des polynômes avec plusieurs variables).
Je vous propose de plonger dans ML-KEM, qui repose sur les lattices et le problème mathématique d’apprentissage modulaire avec erreurs ou Module Learning With Errors (MLWE).

Concepts mathématiques utilisés dans ML-KEM

Afin de comprendre ML-KEM, il est intéressant de comprendre les concepts mathématiques manipulés dans ML-KEM. Si vous détestez vraiment les maths, vous pouvez toujours passer à la section suivante qui traite de ML-KEM mais vous aurez une compréhension partielle. Si vous aimez un peu les maths, ça continue ici !

Lattices

Commençons par les réseaux euclidiens (parfois appelées treillis) ou lattices. Une lattice est un sous-groupe discret d’un espace vectoriel euclidien. Ce dernier est annoté $\mathbb{R}^n$, avec $\mathbb{R}$ l’ensemble des nombres réels, c’est-à-dire les nombres pouvant être représentés sous forme entière et décimale, et $n$ la dimension de l’espace, c’est-à-dire le nombre de coordonnées nécessaires pour représenter les points dans cet espace (on peut se représenter un espace visuellement jusqu’à la 3ème dimension, quand $n$ vaut 3). En d’autres termes, une lattice un ensemble de points arrangés régulièrement dans un espace multi-dimensionnel, selon un motif pouvant se répéter. Avec une dimension de 2 ($n=2$), une lattice est une sorte de grille contenant des points comme montré sur la figure suivante.

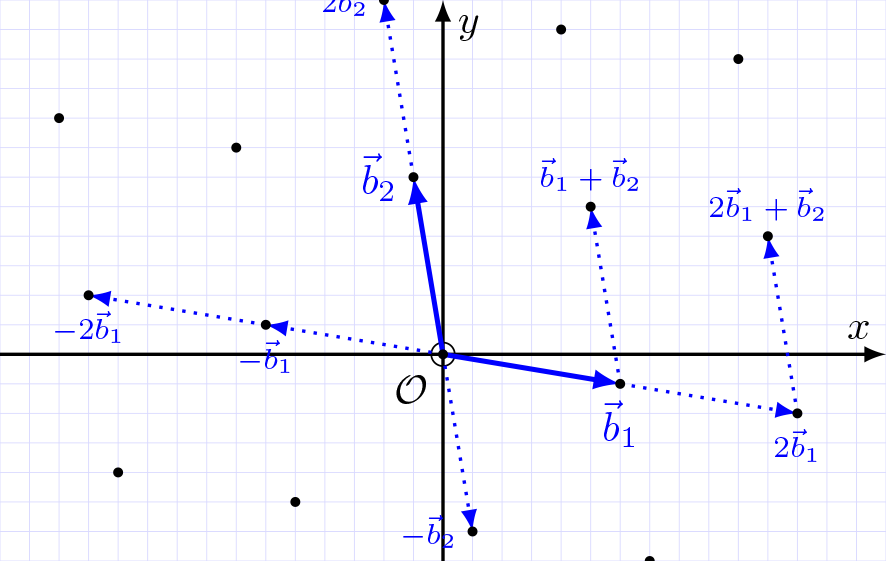
Exemple de lattice de dimension 2 avec une base illustrée (source : https://connect.ed-diamond.com/GNU-Linux-Magazine/glmf-178/une-cryptographie-nouvelle-le-reseau-euclidien)

Une lattice dispose d’une origine qui peut être vue comme une sorte de “point de départ dans la grille” permettant de générer le réseau euclidien. On distingue également la base, un ensemble de vecteurs qui permettent de génerer les autres points et qui peut être vue comme les “règles de déplacement” dans la grille.

Dans ces lattices (surtout à dimension élevée), il existe des problèmes de calculs très difficiles à résoudre (même avec des ordinateurs quantiques), comme le problème du plus court vecteur ou Shortest Vector Problem (SVP), qui consiste à trouver le point le plus proche de la base. On peut aussi citer le problème du plus proche vecteur ou Closest Vector Problem (CVP), qui revient à trouver le point le plus proche d’un point donné. La difficulté pour résoudre ces problèmes est dû au nombre immense de possibilités existantes dans un espace à haute dimension ($n$ très grand). De ce fait, la complexité de SVP et CVP est exponentielle.

LWE et MLWE

L’apprentissage avec erreurs ou Learning With Errors (LWE) consiste à trouver un vecteur secret $s$ dans un espace vectoriel $\mathbb{Z}^n_q$ (l’ensemble de tous les vecteurs de dimension $n$ dont les composantes sont des entiers modulo $q$) de $n$ nombres étant donné $(A, b)$ tel que $b = A \cdot s + e\bmod{q}$, avec $A$ étant une matrice aléatoire, $e$ un vecteur aléatoire et $q$ un nombre premier. Résoudre LWE consiste en quelque sorte à résoudre une instance spécifique du CVP sur un réseau bien particulier. Le cœur de LWE réside dans l’ajout de bruit (le vecteur d’erreur $e$) qui devient alors très complexe comparé à un système sans ce bruit.

Une variante de LWE est Module LWE (MLWE). MLWE opère sur des éléments de modules sur un anneau. Définissons ce qu’est un anneau et un module.

Un anneau ou ring est une structure algébrique (un ensemble et des opérations possibles dans cet ensemble satisfaisant certaines propriétés) contenant un ensemble et deux opérations binaires : addition et multiplication, sauf qu’ici l’addition et la multiplication ne sont pas forcément commutatives, c’est-à-dire que l’ordre des opérandes peut changer le résultat de l’opération. Les anneaux peuvent être variés : anneau de nombre entiers, anneau de polynômes à coefficients réels, anneau de polynômes dont les coefficients sont soumis un modulo… Un polynôme est une expression mathématique formée de produits et de sommes de constantes et de variables.
Un module est un espace vectoriel (ensemble de vecteurs qu’on peut additionner entre eux ou multiplier par un scalaire qui est une quantité tel un nombre qui permet de changer d’échelle) où on peut multiplier les éléments par des scalaires qui proviennent d’un anneau.

Ainsi, alors que LWE opère sur des vecteurs et matrices de nombres entiers, MLWE opère sur des vecteurs et matrices de polynômes et non d’entiers.

L’essence et la force de ML-KEM réside dans MLWE. Voyons donc maintenant comment ML-KEM fonctionne.

ML-KEM

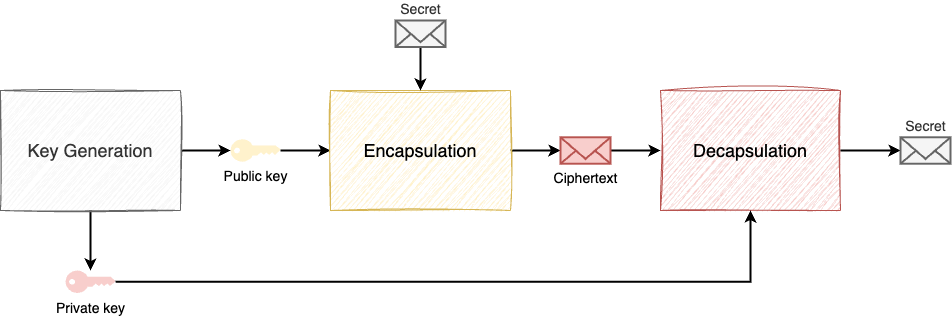
ML-KEM, appelé CRYSTALS-Kyber avant sa standardisation par le NIST, est un mécanisme d’encapsulation de clés ou Key Encapsulation Mechanism (KEM) post-quantique reposant sur MLWE. Un KEM est un mécanisme de cryptographie asymétrique permettant de générer un secret et de le transmettre de manière sécurisé à l’aide d’une paire de clés privé-publique. Cela contient trois étapes :

la génération d’une paire de clés : une clé publique et une clé privée ;
l’encapsulation : génération d’un secret et chiffrement de celui-ci avec la clé publique pour produire un chiffré ou ciphertext ;
la décapsulation : déchiffrement du ciphetext* avec la clé privé afin de retrouver le secret.

ML-KEM utilise l’anneau de polynômes $R_q = \mathbb{Z}_q[X]/(X^n + 1)$, où :

$X^n + 1$ est le modulus polynomial : c’est un polynôme dont les coefficients proviennent de $\mathbb{Z}_q$ (l’ensemble des entiers modulo $q$) et qui sert de modulo dans ML-KEM pour les opérations sur les polynômes eux-mêmes ;
$n$, fixé à $256$, est le degré du polynôme $X^n + 1$ dont les coefficients proviennent de $\mathbb{Z}_q$ (l’ensemble des entiers modulo $q$), $n$ est donc par extension la dimension des polynômes dans l’anneau $R_q$ ;
$q$, nombre premier fixé à $3389$, est un nombre premier qui est le modulo pour les opérations sur les coefficients de chaque polynôme.

C’est dans l’espace de travail $R_q$ que les opérations de ML-KEM ont lieu.
Un autre paramètre, $k$, est la dimension des vecteurs/matrices de polynômes. Plus il est élevé, plus la dimension du problème MLWE sera élevée. La valeur de $k$ permet de faire varier le niveau de sécurité de ML-KEM :

ML-KEM-512 utilise $k = 2$ et propose un niveau de sécurité équivalent à AES-128 ;
ML-KEM-768 utilise $k = 3$ et propose un niveau de sécurité équivalent à AES-192 ;
ML-KEM-1024 utilise $k = 4$ et propose un niveau de sécurité équivalent à AES-256.

Je vous propose de voir désormais les algorithmes de génération de clés, d’encapsulation et décapsulation avec nos amis Alice et Bob. Enfin, nous regarderons de plus près les performances de ML-KEM.

Génération de clés

L’objectif de cette étape est de générer une paire de clés publique-privée. Pour ce faire, Alice créée :

une matrice $A$ de polynômes aléatoires ;
un vecteur d’erreur $e$ de “petits” polynômes (des polynômes dont les coefficients sont beaucoup plus petits que le modulo $q$ : des valeurs comme -2, -1, 0, 1, 2…) ;
un vecteur secret $s$ de polynômes aléatoires : c’est la clé privée d’Alice.

Puis Alice calcule alors $$t = A \cdot s + e \bmod{q}$$
La clé publique est ainsi notée $(A, t)$.

Encapsulation

L’objectif est ici de générer un message secret et de le chiffrer pour le transmettre. Dans cette étape, Bob récupère la clé publique $(A, t)$ d’Alice et créé des vecteurs de bruit $r$, $e_1$ et $e_2$.
On considère un message secret qui servira à dériver une clé de chiffrement AES par exemple, encodé dans un polynôme noté $m$ dont les coefficients représentent les bits du message. Ce polynôme est multiplié par l’arrondi de la moitié de $q$ soit $\left\lfloor \frac{q}{2} \right\rfloor$ afin de faciliter la détection des bits lors de son déchiffrement.
Bob génère alors : $$u = A^T \cdot r + e_1$$ $$v = t^T \cdot r + e_2 + m $$ où $A^T$ est la transposée (matrice inversée) de A et $t^T$ est le transposé (vecteur inversé) de T.

Le chiffré ou ciphertext est ainsi noté $(u, v)$. Il est transmis par Bob à Alice.

Décapsulation

La décapsulation consiste à réaliser le déchiffrement du ciphertext $(u, v)$ par Alice à l’aide de sa clé privée en réalisant l’opération suivante de calcul d’un polynôme $m_n$ : $$m_n = v - s^T \cdot u$$ A partir du polynôme $m_n$ obtenu, Alice “arrondit” chaque coefficient de $m_n$ : soit vers $0$, soit vers $\left\lfloor \frac{q}{2} \right\rfloor$, puis divise par $\left\lfloor \frac{q}{2} \right\rfloor$ afin d’obtenir le polynôme originel $m$ dont elle peut extraire les bits pour connaître le message initial transmis par Bob.

La force réside dans l’ajout de bruit ($r$, $e_1$, $e_2$) pour perturber un attaquant dans toute tentative d’attaque, même avec un ordinateur quantique, mais suffisamment petit pour ne pas empêcher l’acte d’arrondi de garder la distinction des bits sans erreur.

Performance

Je me suis amusé à tester une implémentation de ML-KEM en Python, pqcrypto dont j’ai intégré et testé le calcul de vitesse d’exécution dans mon outil cryptauditor qui permet de mesurer la vitesse d’exécution d’algorithmes de cryptographie. Les mesures ont été effectuées sur un MacBook M4 Pro avec 48 Go de mémoire et tournant sur macOS Sequoia (version 15.5).
J’ai réalisé 1000 fois l’opération d’encapsulation et décapsulation afin de mesurer la vitesse moyenne de ML-KEM-512, ML-KEM-768 et ML-KEM-1024 :

$ python3 cryptauditor.py -K ML-KEM-512 -r 1000 -u us
Performing 1000 rounds of ML-KEM-512 encapsulation and decapsulation
Encapsulation time: 14.802us
Decapsulation time: 19.28us

$ python3 cryptauditor.py -K ML-KEM-768 -r 1000 -u us
Performing 1000 rounds of ML-KEM-768 encapsulation and decapsulation
Encapsulation time: 23.428us
Decapsulation time: 29.665us

$ python3 cryptauditor.py -K ML-KEM-1024 -r 1000 -u us
Performing 1000 rounds of ML-KEM-1024 encapsulation and decapsulation
Encapsulation time: 34.615us
Decapsulation time: 42.664us

On constate que plus le niveau de sécurité augmente et donc plus la dimension des vecteurs / matrices augmente, plus le temps d’exécution augmente de manière linéaire, allant jusqu’à doubler.
J’ai souhaité comparer ML-KEM avec AES et RSA afin d’avoir un ordre d’idée des performances de ML-KEM. Pour AES, j’ai choisi le mode CTR qui ne réalise que le chiffrement et est l’un des plus rapides et sécurisé, et j’ai testé des tailles de clés de 128, 192 et 256 bits qui équivalent respectivement au niveau de sécurité de ML-KEM-512, ML-KEM-768 et ML-KEM-1024. Pour RSA, j’ai choisi une taille de clé de 4096 bits ce qui est considéré robuste avant le post-quantique. Les messages secrets générés et encapsulés par ML-KEM ayant ici une taille de 256 bits (8 octets), j’ai donc chiffré et déchiffré des données d’une taille de 8 octets.

$ python3 cryptauditor.py -c AES-CTR -k 128 -d 8B -r 1000 -u us
Performing 1000 rounds of AES encryption and decryption in CTR mode with a 128-bit random key on 8B of random data
Encryption time: 1.089us
Decryption time: 0.789us

$ python3 cryptauditor.py -c AES-CTR -k 192 -d 8B -r 1000 -u us
Performing 1000 rounds of AES encryption and decryption in CTR mode with a 192-bit random key on 8B of random data
Encryption time: 1.051us
Decryption time: 0.723us

$ python3 cryptauditor.py -c AES-CTR -k 256 -d 8B -r 1000 -u us
Performing 1000 rounds of AES encryption and decryption in CTR mode with a 256-bit random key on 8B of random data
Encryption time: 1.105us
Decryption time: 0.756us

$ python3 cryptauditor.py -c RSA -k 4096 -d 8B -r 1000 -u us
Performing 1000 rounds of RSA-OAEP encryption and decryption with a 4096-bit random key on 8B of random data
Encryption time: 914.504us
Decryption time: 8446.101us

On constate que AES est bien plus rapide que ML-KEM (plusieurs dizaines de fois plus rapide), ce qui est attendu. En effet, AES est un algorithme de chiffrement symétrique des données, là ou ML-KEM est utilisé pour l’échange de clés. En revanche, on voit que ML-KEM est de l’ordre de plusieurs dizaines à centaines de fois plus rapide que RSA !

Conclusion

Nous avons découvert ensemble dans cet article ce qu’est la cryptographie post-quantique avec l’échange de clés ML-KEM. Nous avons répondu aux questions suivantes que nous avons posé en début d’article :

Qu’est-ce qu’un ordinateur quantique ?
Finalement, un ordinateur qui fonctionne avec des propriétés physiques différentes des ordinateurs classiques lui permettant de démultiplier sa puissance de calcul.
Pourquoi l’ordinateur quantique menace-t-il la cryptographie actuelle ?
Car cette nouvelle puissance de calcul permet d’élaborer de nouveaux algorithmes cassant les problèmes mathématiques du logarithme discret et de la factorisation de nombres premiers, utilisés dans la cryptographie actuelle.
En quoi la cryptographie post-quantique diffère-t-elle de la cryptographie actuelle ?
Ce sont toujours des mathématiques derrière, mais avec l’exploration de problèmes résistants aux algorithmes post-quantiques.
Comment la cryptographie post-quantique peut-elle se protéger de l’ordinateur quantique ?
Par l’utilisation d’algorithmes résidant sur des notions dont les problèmes sont théoriquement impossible à casser même avec un ordinateur quantique : basés sur les lattices, basés sur les fonctions de hachage, etc.

Au moment d’écrire cet article, la cryptographie post-quantique est encore jeune et assez peu déployée à grande échelle et il faudra donc du recul bien sûr, après l’arrivée des ordinateurs quantiques. En attendant, la recommandation est un emploi hybride, c’est-à-dire la combinaison de cryptographie post-quantique et cryptographie classique. Par exemple, il s’agit de l’utilisation de ML-KEM en combinaison de Elliptic Curve Diffie-Hellman (ECDH) pour générer et échanger des secrets partagés.

Enfin, je concluerai en disant qu’il est temps de s’y mettre ! Je vous encourage donc fortement à consulter les ressources ci-dessous.

Sources

Cloudflare Radar : https://radar.cloudflare.com/embed/PostQuantumXY?dateRange=52w&botClass=LIKELY_HUMAN&widgetState=%7B%22showAnnotations%22%3Afalse%2C%22xy.hiddenSeries%22%3A%5B%5D%2C%22xy.highlightedSeries%22%3Anull%2C%22xy.hoveredSeries%22%3Anull%2C%22xy.previousVisible%22%3Atrue%7D&ref=%2Fadoption-and-usage. Consulté le 03/07/2025.
Cloudflare Research - Post-Quantum Key Agreement at Cloudflare : https://pq.cloudflareresearch.com/. Consulté le 03/07/2025.
Polytechnique insights - La physique quantique expliquée par l’un de ses prix Nobel : https://www.polytechnique-insights.com/tribunes/science/la-physique-quantique-expliquee-par-lun-de-ses-prix-nobel/. Consulté le 03/07/2025.
Wikipédia - Chat de Schrödinger : https://fr.wikipedia.org/wiki/Chat_de_Schr%C3%B6dinger. Consulté le 03/07/2025.
Jean-Philippe AUMASSON, Serious Cryptography - No Starch Press, 312 pages, 2017.
QNu Labs - Quantum 101 - What is a Qubit? : https://www.qnulabs.com/blog/quantum-101-qubit. Consulté le 03/07/2025.
CERN - Les expériences LHC au CERN observent l’intrication quantique à une énergie inédite : https://home.cern/fr/news/press-release/physics/lhc-experiments-cern-observe-quantum-entanglement-highest-energy-yet. Consulté le 03/07/2025.
Wikipédia - États de Bell : https://fr.wikipedia.org/wiki/%C3%89tats_de_Bell. Consulté le 03/07/2025.
Yao, Y.; Xiang, L. Superconducting Quantum Simulation for Many-Body Physics beyond Equilibrium. Entropy 2024, 26, 592. https://doi.org/10.3390/e26070592
Thibaut Probst - Découvrir les courbes elliptiques en cryptographie : https://thibautprobst.fr/posts/elliptic-curves. Consulté le 03/07/2025.
Fraunhofer AISEC - A (somewhat) gentle introduction to lattice-based post-quantum cryptography : https://www.cybersecurity.blog.aisec.fraunhofer.de/en/a-somewhat-gentle-introduction-to-lattice-based-post-quantum-cryptography/. Consulté le 03/07/2025.
Connect - Une cryptographie nouvelle : le réseau euclidien : https://connect.ed-diamond.com/GNU-Linux-Magazine/glmf-178/une-cryptographie-nouvelle-le-reseau-euclidien. Consulté le 03/07/2025.
ANSSI - Guide des mécanismes cryptographiques - Règles et recommandations concernant le choix et le dimensionnement des mécanismes cryptographiques : https://cyber.gouv.fr/sites/default/files/2021/03/anssi-guide-mecanismes_crypto-2.04.pdf. Consulté le 03/07/2025.
National Institute of Standards and Technology (2024) Module-Lattice-Based KeyEncapsulation Mechanism Standard. (Department of Commerce, Washington, D.C.), Federal Information Processing Standards Publication (FIPS) NIST FIPS 203. https://doi.org/10.6028/NIST.FIPS.203. Consulté le 03/07/2025.
YouTube - Cryptography 101 - Short course on Kyber and Dilithium by Alfred Menezes : https://www.youtube.com/watch?v=9NKm84vKALc&list=PLA1qgQLL41SSUOHlq8ADraKKzv47v2yrF. Consulté le 03/07/2025.
Gicquel A.; Brenner, A.; Sepe, B. Retour d’expérience sur la montée en compétence d’un cabinet d’audit en cryptographie post-quantique. SSTIC 2025 : https://www.sstic.org/media/SSTIC2025/SSTIC-actes/retour_dexprience_sur_la_monte_en_comptence_dun_ca/SSTIC2025-Article-retour_dexprience_sur_la_monte_en_comptence_dun_cabinet_daudit_en_cryptographie_post-quantique-br_QocDuAb.pdf.
PyPI - pqcrypto : https://pypi.org/project/pqcrypto/. Consulté le 03/07/2025.
GitHub - thibaut-probst : cryptauditor : https://github.com/thibaut-probst/cryptauditor. Consulté le 03/07/2025.
Thibaut Probst - Choisir le mode d’opération pour chiffrement par bloc : https://thibautprobst.fr/posts/block-cipher. Consulté le 03/07/2025.