Découvrir les courbes elliptiques en cryptographie

07/05/2023 · 21 mins de lecture · cybersecurite cryptographie ecc courbeselliptiques ellipticcurves keyexchange ecdh signature ecdsa chiffrement encryption ecies cryptauditor  ·
Partager sur:

Traductions

Sommaire

Dans cet article, je vous invite à plonger une nouvelle fois avec moi dans l’univers de la cryptographie, et cette fois-ci pour découvrir et comprendre un concept qui peut paraître obscur : les courbes elliptiques en cryptographie. En effet, l’énoncé du terme courbes elliptiques sous-entend l’utilisation de mathématiques, ce qui en rebute certains. L’objectif de cet article est ainsi de vous permettre de comprendre le concept des courbes elliptiques de manière simplifiée et de voir leur application en cryptographie pour l’échange de clés, les signatures numériques ou encore le chiffrement.

Introduction

La cryptographie est omniprésente pour sécuriser nos données. Grâce à elle, on arrive à garantir des propriétés essentielles telles que :

  • la confidentialité des données : l’information ne peut être lue par une personne non autorisée ;
  • l’intégrité des données : l’information ne peut être modifiée par une personne non autorisée ;
  • l’authenticité des données : l’information est attribuée à son auteur légitime ;
  • la non-répudiation des données : l’information ne peut faire l’objet d’un déni de la part de son auteur.

De nombreuses, techniques, méthodes, protocoles et algorithmes existent pour chiffrer (garantissant la confidentialité), calculer des empreintes (garantissant l’intégrité voire l’authenticité) ou signer (garantissant l’intégrité, l’authenticité et la non-répudiation) les données. Parmi ces moyens, la cryptographie asymétrique ou cryptographie à clé publique est un ensemble de méthodes pour assurer la confidentialité, l’authenticité ou la non-répudiation des données à partir d’une clé privée (non divulguée par l’entité la possédant) et d’une clé publique (divulguée aux entités communiquant avec l’entité la possédant).
Ces moyens font appel aux mathématiques, discipline abstraite manipulant les nombres, les fonctions, la géométrie, les plans, les espaces… Parmis ces objets, les courbes elliptiques furent intégrées en 1985 dans la cryptographie et largement utilisées à partir des années 2000.
D’abord, nous nous rafraîchirons la mémoire sur la géométrie, les courbes et les équations afin de mieux appréhender ensuite les courbes elliptiques et comment faire des opérations dessus. Puis, nous approfondierons comment les courbes elliptiques sont utilisées en cryptographie pour chiffrer des données, échanger des clés de chiffrement ou bien signer des données.

Bon vous l'aurez compris, on va faire un peu de maths !

Géométrie, courbes et équations

Une courbe elliptique est un objet mathématique qui appartient à la géométrie algébrique : c’est une courbe algébrique. Pas de panique, on va expliciter tous ces termes farfelus !

La géométrie d’abord, c’est l’étude des figures dans un espace ou sur un plan. Il existe plusieurs types de géométrie : euclidienne (probablement la plus connue, abordée en premier dans la scolarité), affine, projective, différentielle… En fait, à chaque géométrie est associé un contexte incluant des techniques propres à certaines branches des mathématiques, afin d’étudier des formes et leurs propriétés multiples. Par exemple, dans la géométrie euclidienne, on étudie les points, les droites, les segments, les angles, les surfaces, les volumes, etc. à partir des axiomes (sortes d’assertions servant la théorie) d’Euclide.

La géométrie algébrique ensuite, c’est une géométrie qui étudie des figures composées de points dont les coordonnées sont régies par des équations n’utilisant que des sommes (résultats d’additions) et des produits (résultats de multiplications).
Une courbe elliptique justement, c’est une courbe dîte algébrique et définie par une équation de forme bien particulière. Et si on se rafraîchissait les idées sur les équations du coup ?

Une équation mathématique, c’est une expression (un ensemble de nombres, de variables et d’opérateurs) qui décrit une égalité en impliquant une ou plusieurs variables ou inconnues (représentées généralement par des lettres), c’est-à-dire des nombres dont on ne connait pas la valeur. Ces nombres dont on cherche la ou les valeurs sont les solutions de l’équation.
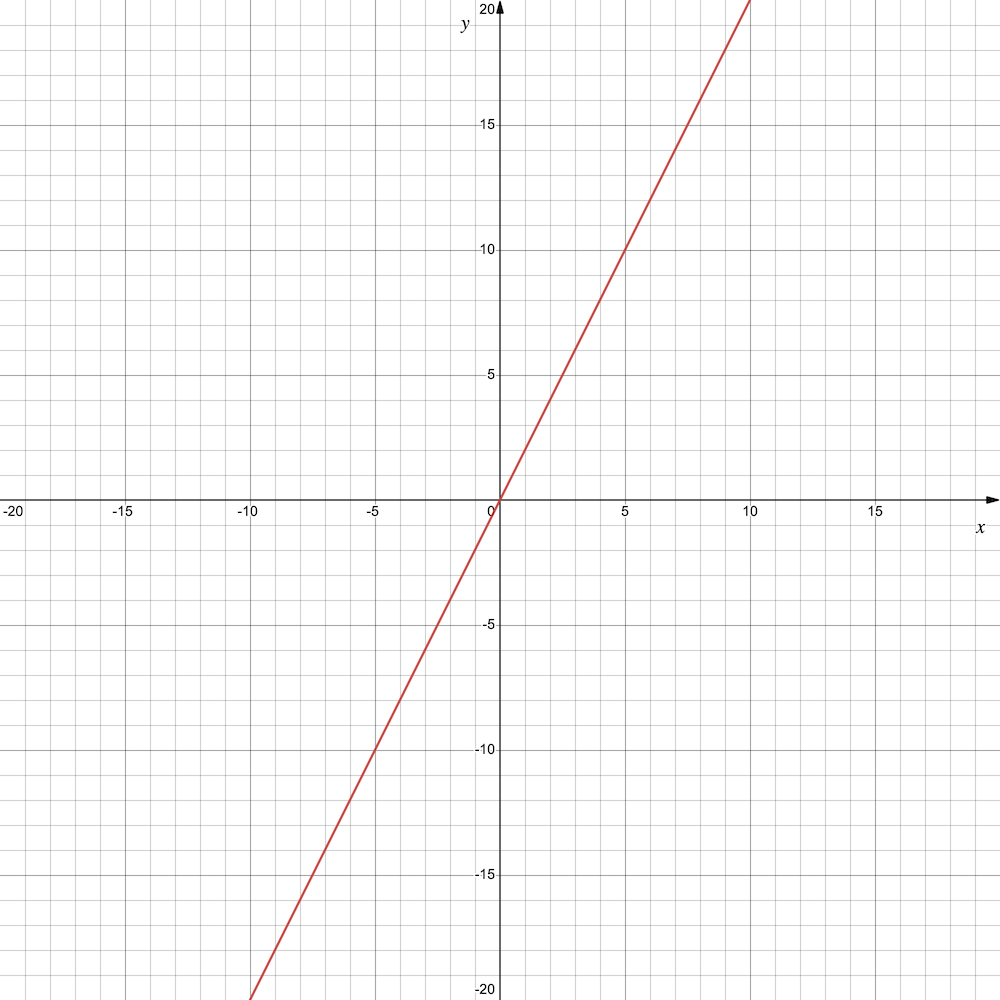
Par exemple, voici une équation mathématique : $ y = 2x $. Ici, on dit que la variable $y$ vaut deux fois la valeur de la variable $x$. Il y a plein de solutions, comme par exemple : $ y = 2, x = 1 $. Si on s’amuse à tracer une courbe qui dessine les valeurs d’$y$ (les ordonnées) en fonction de celles de $x$ (les absisses) dans le plan, cela donne une droite :

Courbe d’'équation $y = 2x$

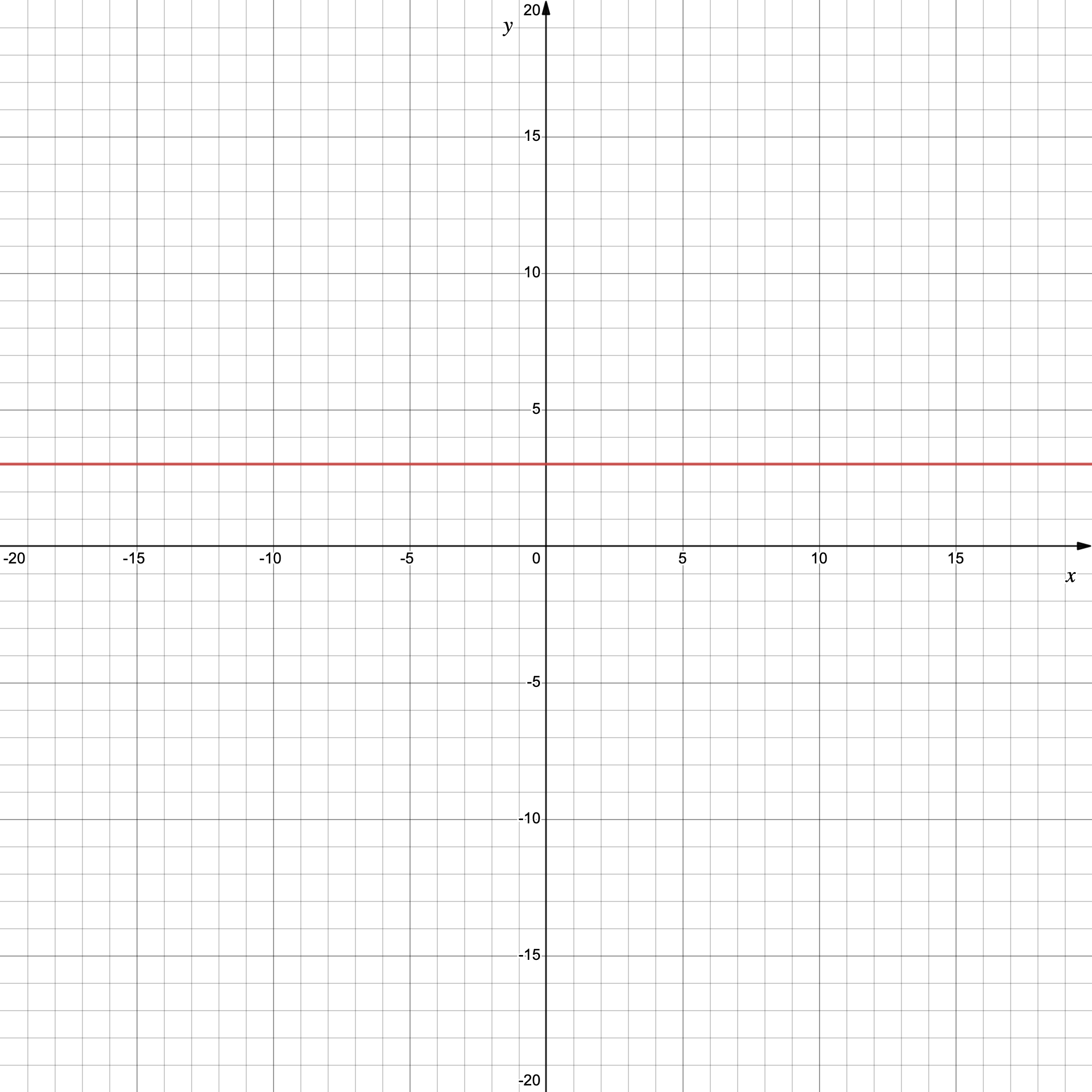
Prenons un autre exemple d’équation : $ y = 3 $. C’est une équation très simple ou $y$ est toujours égal à 3 (il n’y a pas de variable $x$ !) avec une courbe qui est alors une droite horizontale :
Courbe d’'équation $y = 3$

Bon, OK, et les courbes elliptiques dans tout ça ?

Courbes elliptiques et opérations

Maintenant que nous sommes au point sur ce qu’est une courbe et une équation, venons-en aux courbes elliptiques.

Courbes elliptiques et équation de Weierstrass

Une courbe elliptique est une courbe algébrique dont les points traçant la courbe sont placés selon une équation de la forme $y^2 = x^3 + ax + b$. On appelle cela la forme de Weierstrass (du nom d’un mathématicien allemand du XIXème siècle). En plus de $x$ et $y$, on a ici deux autres paramètres $a$ et $b$. Le carré d’$y$ ($y$ multiplié par lui-même) est égal au cube de $x$ ($x$ multiplié 2 fois par lui-même) auquel on ajoute $a$ multiplié par $x$ et auquel on ajoute $b$. $a$ et $b$ sont des valeurs constantes qu’on fixe, ce qui nous permet de pouvoir définir des courbes elliptiques de formes différentes. En gros, en faisant varier $a$ et $b$, la courbe change de forme.
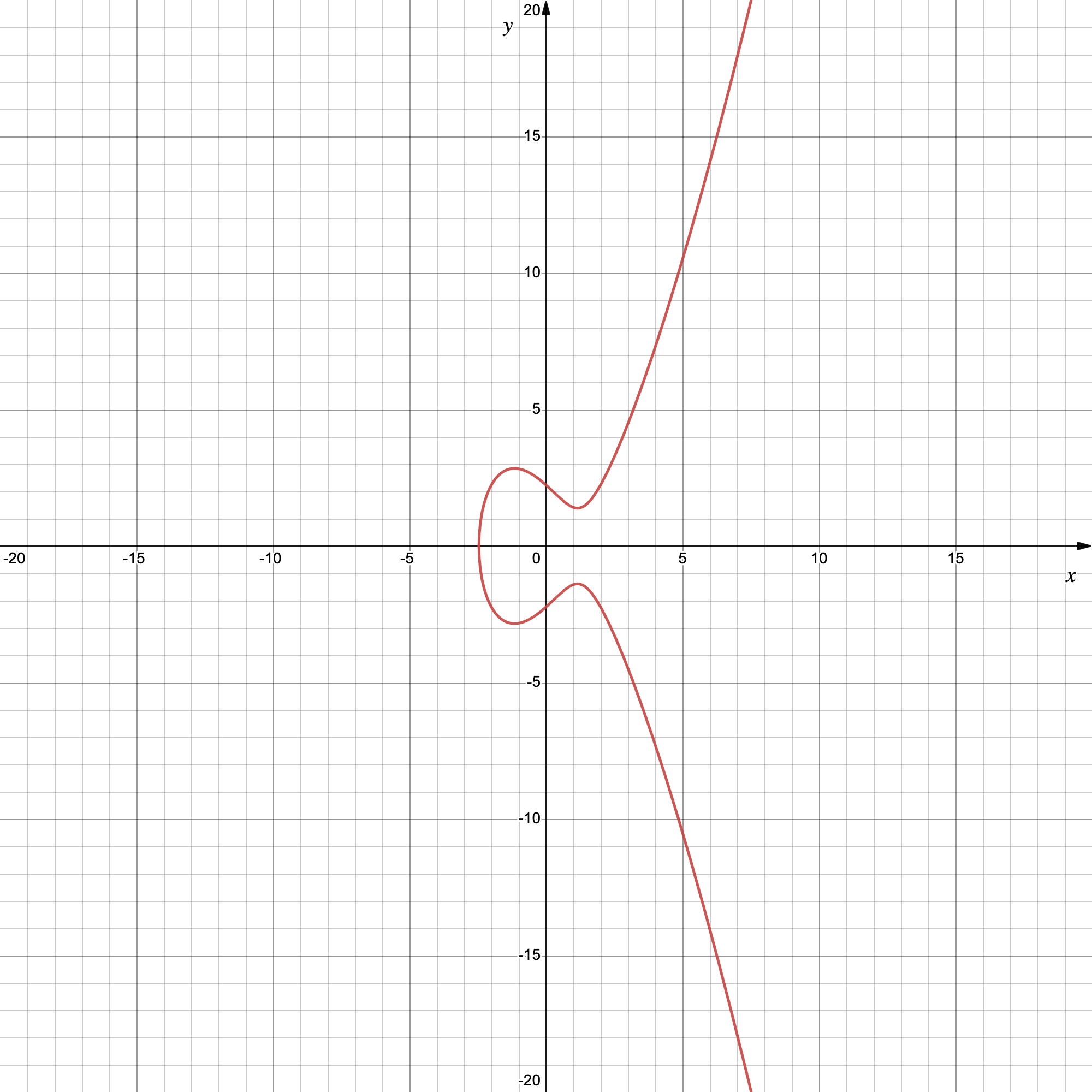
Si on fixe $a = -4$ et $b = 5$, on a donc une équation de la forme $y^2 = x^3 -4x + 5$. Le dessin associé donne :

Courbe d’'équation $y^2 = x^3 -4x + 5$

Si on prend $a = -6$ et $b = 2$, on a donc une équation de la forme $ y^2 = x^3 -6x + 2 $. Le dessin associé donne :

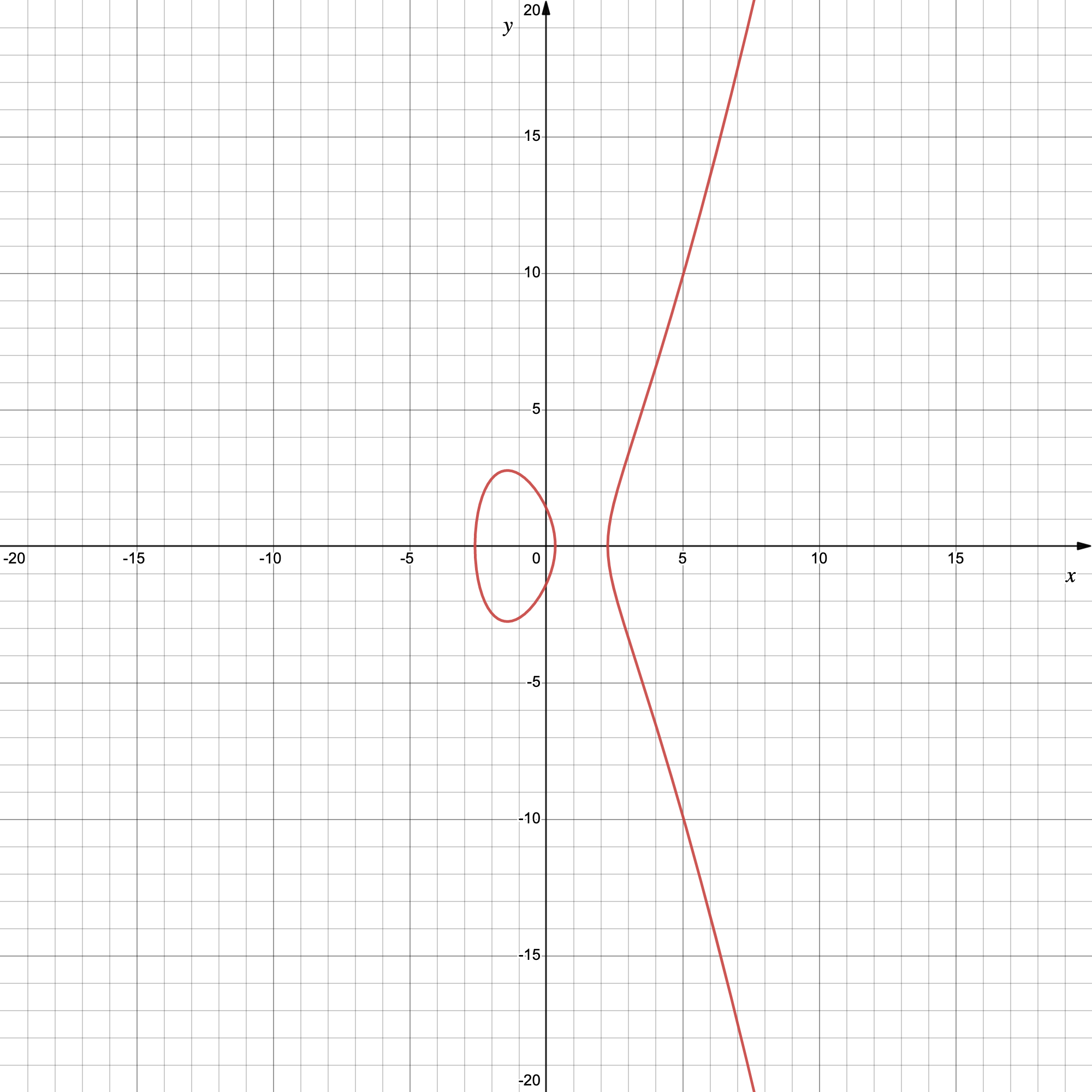
Courbe d’'équation $y^2 = x^3 -6x + 2$

Hmm… pas vraiment “elliptique” tout ça ? Et bien non. Les courbes elliptiques ressemblent effectivement plus à des cercles et des paraboles… Le terme “elliptique” vient du fait que les courbes elliptiques ont émergé de l’étude du calcul d’intégrales elliptiques, initialement utilisé pour déterminer la longueur d’arc d’une ellipse.

L'orbite des planètes est finalement plus elliptique que les courbes elliptiques

Les courbes elliptiques ont des propriétés géométriques intéressantes notamment car on peut mener des additions et des multiplications sur ces courbes.

Addition sur courbes elliptiques

Une addition sur une courbe elliptique, cela revient à séléctionner sur la courbe deux points, notés par exemple $P$ et $Q$, puis tracer une droite entre ces deux points, et à l’intersection de cette droite avec la courbe, noté $R$, il suffit choisir le point à l’opposé, noté $R’$, c’est-à-dire le point dont la valeur $x$ de coordonnés est l’opposé du point $R$. Cette méthode est illustrée ci-dessous.

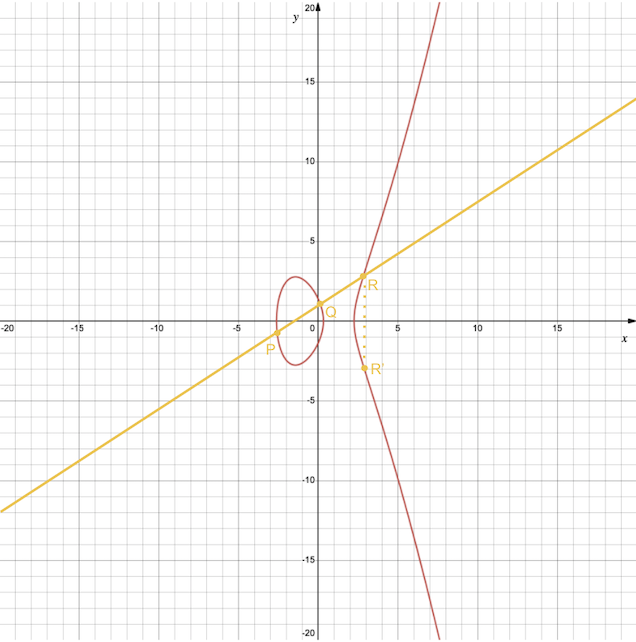
Règle géométrique pour additionner deux points sur une courbe elliptique

Je vous passe le détail des calculs mathématiques pour déterminer les coordonnées de $R’$. La règle géométrique pour trouver $P + Q = R’$ est bien pratique mais ne fonctionne pas dans tous les cas de figure.
En effet, que se passe-t-il si les points $P$ et $Q$ se situent au même endroit ($P = Q$) ? Si $P$ et $Q$ sont confondus, on veut donc ajouter $P$ à $P$ et la technique pour additioner $P$ avec $P$ est de tracer une tangente pour trouver $R$ et en déduire $R’$ son opposé qui est le résultat de $P + P = 2P$.

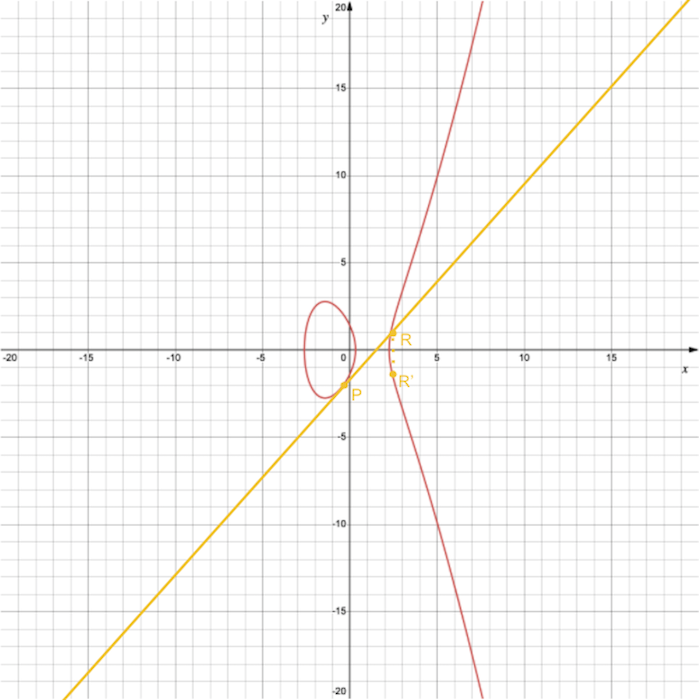
Règle géométrique pour additionner deux points confondus sur une courbe elliptique

Que se passe-t-il si $P$ et $Q$ sont sur la même abscisse (valeurs de coordonnées $x$ égales) ? Et bien la droite qu’on peut tracer est alors une droite verticale qui ne croise jamais la courbe pour trouver $R$ puis $R’$. On définit alors un point dit à l’infini et noté $O$ tel que $P + O = P$ soit $P + (-P) = O$.

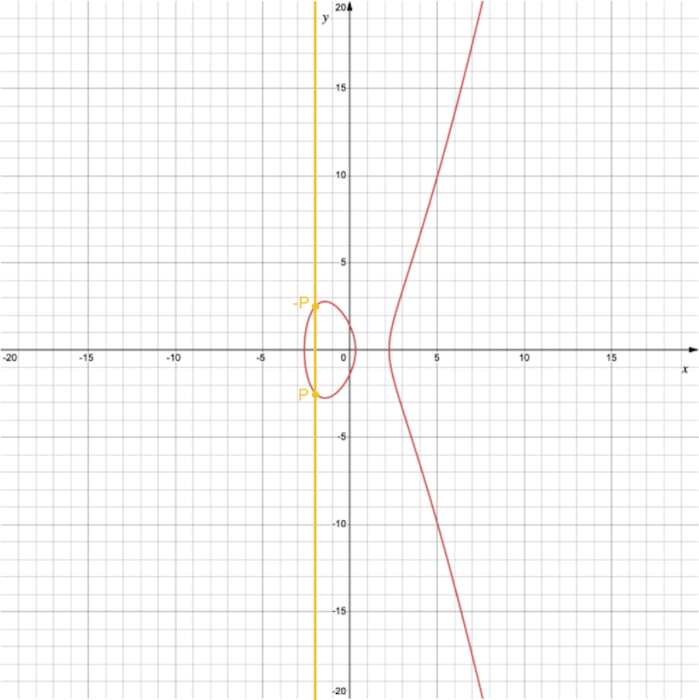
Règle géométrique pour additionner deux points de même abscisse sur une courbe elliptique

Multiplication sur courbes elliptiques

Une multiplication, c’est une série d’additions. En effet, si on fait $2 \times 3$, on fait $2 + 2 + 2 $ ou bien $3 + 3$ pour trouver $6$. Sur une courbe elliptique, si on multiplie un point $P$ par une valeur $k$ (on fait donc $k \times P$ ou $kP$), on pourrait répéter $k - 1$ fois l’opération $P + P$. Mais il y a plus efficace, surtout si $k$ est un nombre très grand. On peut regrouper les opérations pour en réduire le nombre total. Par exemple, si $k$ vaut $16$, on pourrait naïvement procéder à $16 - 1 = 15$ opérations pour calculer $kP$ : $16P = P + P + P + P + P + P + P + P + P + P + P + P + P + P + P + P$. Cependant, on peut en fait procéder de la sorte :

  • Calcul de $P_{1} = P + P$
  • Calcul de $P_{2} = P_{1} + P_{1}$
  • Calcul de $P_{3} = P_{2} + P_{2}$
  • Calcul de $P_{4} = P_{3} + P_{3} = 16P$

Avec 4 opérations d’addition au lieu de 15, on trouve le même résultat !

Courbes elliptiques en cryptographie

On a vu ce que sont les courbes elliptiques et comment réaliser des opérations d’additions et de multiplications sur celles-ci. Alors comment tout cela est utilisé en cryptographie ?

Courbes elliptiques sur corps fini

Jusqu’à présent, nous avons analysé des courbes qui se dessinent avec l’ensemble de nombres réels. Cet ensemble est noté ${R}$ et regroupe les nombres pouvant être représentés sous forme entière et décimale, comme par exemple : $103.00000032$, $0$, $5$, $-4.7524454$, $\frac{3}{2}$… Or, en cryptographie, c’est l’ensemble des nombres entiers (exemples : $0$, $1$, $-6$, $4$, $16$, $19$, etc.), noté ${Z}$, qui est utilisé. On parle donc d’un corps (ou champ) fini. Mais on ne s’arrête pas là, on utilise les nombres entiers modulo un certain nombre premier, qu’on peut appeler $p$, c’est-à-dire un corps premier. Oups, ça veut dire quoi tout ça ?
Plus simplement, ça veut dire que la courbe elliptique va se dessiner avec un ensemble de nombres entiers modulo un nombre $p$. On note cet ensemble ${Z_p}$. Le modulo est une opération mathématique (dénotée $\bmod$) qui permet de calculer le reste d’une division euclidienne de deux entiers. Par exemple, $5\bmod{2} = 1$, car peut mettre deux fois $2$ dans $5$ et il reste alors $1$ : $5 - 2 \times 2 = 1$. Un autre exemple, $378 \bmod{59} = 24$, car on peut mettre six fois $59$ dans $378$ et il reste alors $24$ : $378 - 6 \times 59 = 24$.
Revenons-en à nos courbes elliptiques. Quand on dessine la courbe elliptique d’équation $ y^2 = x^3 -6x + 2 $ dans ${Z_{59}}$, l’ensemble des valeurs possibles est borné entre $0$ et $59$ et on obtient alors une sorte de nuage de points.

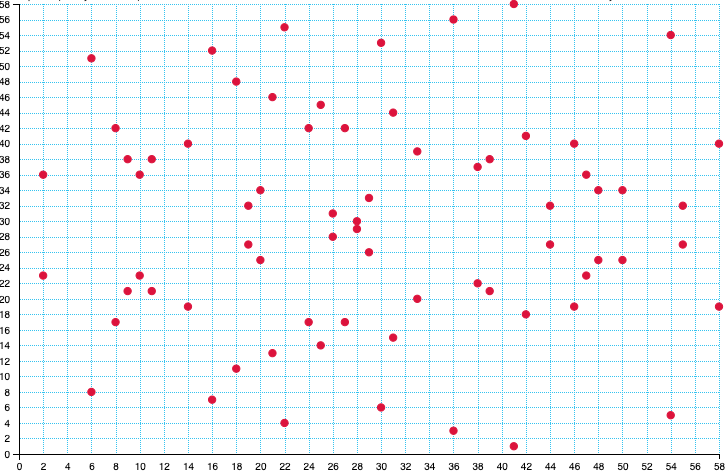
Cela ressemble de moins en moins à une ellipse

En effet, il n’y a plus de vraie courbe lisse puisqu’on ne manipule que quelques valeurs (les nombres entiers) sur une plage donnée (le modulo) et non plus une infinité (les nombres réels). En outre, le modulo “rebouclant” les valeurs dans le corps fini, les points bourgeonnent alors dans l’ensemble.

L’ensemble des points forment ce qu’on appelle un groupe. Le nombre de points dans un groupe s’appelle la cardinalité. Au final, la cardinalité dépend de l’équation choisie (les valeurs de $a$ et $b$ fixées) et de la valeur de $p$. Les opérations sur courbes abordées précedemment restent valables dans cet ensemble.

Nous savons ce qu’est une courbe elliptique, comment faire des opérations dessus et nous sommes désormais conscients de comment elles sont dérivées des courbes algébriques pour pouvoir être employées dans le cadre de la cryptographie à clés publiques.

Types de courbes elliptiques proposées en cryptographie

Plusieurs initiatives ont proposé des courbes pour la cryptographie. Voici les plus répandues.

On peut notamment citer les courbes du National Institute of Standards and Technology (NIST) qui propose des courbes elliptiques sur corps premier et des courbes sur polynômes binaires (expressions mathématiques dont les coefficients sont des valeurs binaires : $0$ ou $1$). La plus célèbre est la courbe P-256 d’équation $y^2 = x^3 - 3x + b$, où $b$ est une constante codé sur 256 bits (un nombre très grand donc). Cette courbe utilise un paramètre de modulo $p$ codé sur 256 bits où $p = 2^{256} - 2^{224} - 2^{192} - 2^{96} - 1$, ce qui vaut aussi un nombre très grand : $$115792089237316195423570985008687907853269984665640564039457584007913129639935$$.
D’autres courbes NIST sont proposées sur 192, 224, 384 et 521 bits.

Il y a également la courbe Curve25519 proposée par Daniel J. Bernstein, dont l’équation est $y^2 = x^3 + 486662x^2 + x$ et utilise un modulo $p = 2^{255} - 19$. L’équation ne ressemble pas exactement à ce que nous avons vu jusqu’à présent mais appartient tout de même à la famille des courbes elliptiques. Cette courbe offre des performances logicielles très intéressantes et se trouve très largement utilisée.

Enfin, citons la courbe Curve448, développé par Mike Hamburg, dont l’équation est $y^2 = x^3 + 156326x^2 + x$ et qui utilise un modulo $p = 2^{448} - 2^{224} - 1$. Cette courbe est donc définie sur 448 bits et se veut très performante.

Problème du logarithme discret sur courbes elliptiques

Un algorithme de cryptographie cherche à rendre un problème insoluble pour toute personne (un attaquant par exemple) qui ne possède pas légitimement les éléments nécessaires pour y parvenir, généralement des clés. Un problème bien connu en cryptographie est celui du logarithme discret ou Discrete Logarithm Problem (DLP). Cela consiste, si on connaît une valeur $A$, à trouver une valeur $a$ telle que $A = g^a\bmod{p}$ (élever $g$ à la puissance $a$ s’appelle une exponentiation) avec $g$ un nombre donné et $p$ un nombre premier très grand. Il est extrêmement difficile de retrouver $a$. Ce problème est notamment utilisé par le protocole d’échange de clés Diffie-Hellman (DH). Il permet à deux entités (souvent appelées Alice et Bob dans les contenus pédagogiques de cryptographie) de se mettre d’accord sur un secret commun sans se le transmettre explicitement, ce qui est très couramment utilisé dans les protocoles réseau pour échanger une clé de chiffrement symétrique :

  • Alice et Bob (non, je n’ai pas été original du coup) choisissent un nombre $p$ premier et un nombre $g$.
  • Alice choisit un nombre $a$ qu’elle garde secret.
  • Alice calcule $A = g^{a}\bmod{p}$ et l’envoie à Bob. Même si un attaquant intercepte $A$, il ne pourra pas retrouver le nombre secret $a$.
  • Bob choisit un nombre $b$ qu’il garde secret.
  • Bob calcule $B = g^{b}\bmod{p}$ et l’envoie à Alice. Même si un attaquant intercepte $B$, il ne pourra pas retrouver le nombre secret $b$.
  • Alice calcule le secret $s = g^{ba}\bmod{p} = g^{ba}\bmod{p}$ de son côté et Bob calcule le même secret $s = g^{ab}\bmod{p} = g^{ab}$ de son côté.

Le tour est joué. Alice et Bob sont en possession du même secret partagé. Je vous conseille la page Wikipédia associée, où on peut comprendre cela avec des échanges de couleurs en plus des nombres.
On a ici manipulé des nombres, alors que l’emploi des courbes elliptiques en cryptogaphie énonce un problème similaire mais en manipulant des courbes, où, à partir d’un point $P$ de la courbe, on cherche à trouver le nombre $k$ tel que $Q = kP$. Ce problème s’appelle le problème du logarithme discret sur courbes elliptiques ou Elliptic Curve Discrete Logarithm Problem (ECDLP). Les différences avec le DLP sont l’utilisation de points sur une courbe elliptique plutôt que des nombres, et l’usage de la multiplication au lieu de l’exponentiation. Les paramètres à choisir sont le type d’équation (choisir $a$ et $b$) et le nombre premier $p$. C’est de cela que dépend le nombre de points présent dans le nuage de points qu’est la courbe elliptique. Plus il y a de points (plus la cardinalité est grande), plus le niveau de sécurité est elevé car le problème (ECDLP) est complexe à résoudre. L’avantage d’ECDLP par rapport à DLP est l’utilisation de nombres plus petits.
Maintenant, voyons dans quelles applications cryptographiques ECDLP est utilisé concrètement.

Echange de clés ECDH

L’adaptation du protocole Diffie-Hellman pour l’échange de clés en intégrant les courbes elliptiques s’appelle Elliptic Curve Diffie-Hellman (ECDH) et s’avère un protocole finalement assez simple :

  • Alice et Bob (encore eux !) choisissent une courbe elliptique (ils fixent $a$ et $b$), le nombre premier $p$ (le modulo) et un point $G$ (la lettre $G$ - du point $G$ - choisie vient du mot “générateur”, rien d’autre…) sur la courbe.
  • Alice choisit un nombre $a$ qu’elle garde secret.
  • Alice calcule le point $A = aG$ et l’envoie à Bob.
  • Bob choisit un nombre $b$ qu’il garde secret.
  • Bob calcule le point $B = bG$ et l’envoie à Alice.
  • Alice calcule le secret $s = aB = abG$ de son côté et Bob calcule $s = bA = baG$ de son côté.

Le tour est joué. Alice et Bob sont en possession du même secret partagé mais en ayant opéré sur une courbe elliptique. Ici, j’ai noté les points calculés sur la courbe $A$ et $B$ pour changer un peu de $P$ et $Q$…

Signatures numériques ECDSA

Les signatures numériques permettent de valider l’authenticité et la non-répudiation d’un document éléctronique et sont très répandues dans notre quotidien : certificat numérique d’un site Web, email, logiciel… Les signatures numériques reposent sur la cryptographie à clés publiques. La signature est générée à partir d’une empreinte du document (calculée avec une fonction de hachage) en chiffrant cette empreinte avec la clé privée du signataire. Elle est envoyée avec le document. Le récepteur peut alors vérifier la signature en la déchiffrant avec la clé publique du signataire et comparer l’empreinte obtenue avec celle du document qu’il recalcule de son côté. Si les empreintes sont les mêmes, la signature est alors valide.

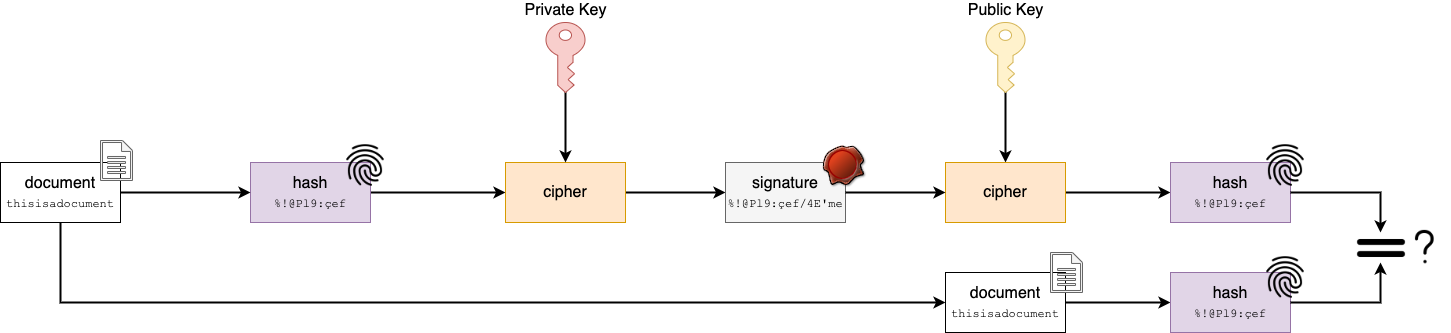
Processus de signature numérique et vérification

Plusieurs algorithmes existent pour la génération et vérification de signatures. On peut notamment citer les algorithmes Digital Signature Algorithm (DSA) ou Rivest–Shamir–Adleman Probabilistic Signature Scheme (RSA-PSS).
Avec les courbes elliptiques, on retrouve deux principaux algorithmes : Elliptic Curve Digital Signature Algorithm (ECDSA) et Edwards-curve Digital Signature Algorithm (EdDSA). Je vous propose d’analyser ECDSA, qui est largement utilisé dans des protocoles réseau comme Transport Layer Security (TLS) ou Secure SHell (SSH), ou encore les transactions de cryptomonnaies telles que le bitcoin.
La génération de signature sur courbes elliptiques avec ECDSA donne le procédé suivant (il faut s’accrocher un peu mais j’ai fait un schéma plus bas) :

  • Alice, le signataire, et Bob, le récepteur, choisissent une courbe elliptique (ils fixent $a$ et $b$), le nombre premier $p$ (le modulo) et un point $G$ sur la courbe. On en déduit $n$ le nombre de points sur la courbe.
  • Alice possède une clé privée qui est en fait un nombre $d$.
  • Bob a connaissance de la clé publique d’Alice qui correspond à un point $P = dG$.
  • Alice génère une empreinte du document à signer à l’aide d’une fonction de hachage. Cette empreinte, notée $h$, est assimilée à un nombre compris entre $0$ et $n-1$.
  • Alice choisit un nombre aléatoire $k$ compris entre $1$ et $n - 1$ et calcule $Q = kG$, un point sur la courbe dont les coordonnées sont notées $(x, y)$. Ici $k$ est donc un nonce (un nombre aléatoire ou pseudo-aléatoire utilisé une seule fois), qui rend le processus probabiliste et non déterministe.
  • Alice calcule $r = x\bmod{n}$ ainsi que $s = \frac{h + rd}{k}\bmod{n}$.
  • La signature du document est alors le couple de valeurs $(r, s)$ et est envoyée à Bob avec le document.
    Notez que la taille de la signature est directement dépendante de la taille des coordonnées utilisées pour la courbe. Par exemple, si la courbe est définie sur 256 bits, $r$ et $s$ auront chacun une taille de 256 bits, donnant une signature de 256 + 256 = 512 bits.

Pour vérifier une signature $(r, s)$ d’un document, voici ce que doit faire Bob (on s’accroche encore un peu, le schéma n’est pas loin):

  • Bob génère une empreinte du document reçu, qu’on note $h$.
  • Bob calcule $Q = \frac{h}{s}G + \frac{r}{s}P$, où $P$ (qui vaut $dG$) est la clé publique d’Alice, connue de Bob et $G$ est le point de base sur la courbe. On peut donc écrire $Q = \frac{h+rd}{s}G$.
  • Dans son calcul de $Q$, Bob remplace $s$ par sa valeur (pour rappel, $s = \frac{h + rd}{k}\bmod{n}$) : $Q = kG$.
  • Si l’empreinte du document $h$ recalculée par Bob est la bonne, à partir de la signature (contenant l’empreinte calculée par Alice et l’abscisse de $Q$ calculé par Alice) et la clé publique d’Alice, si $Q$ (de coordonnées $(x, y)$) recalculé par Bob a une abscisse $x$ de même valeur que le $x$ transmis via la signature par Alice, alors la signature est valide.

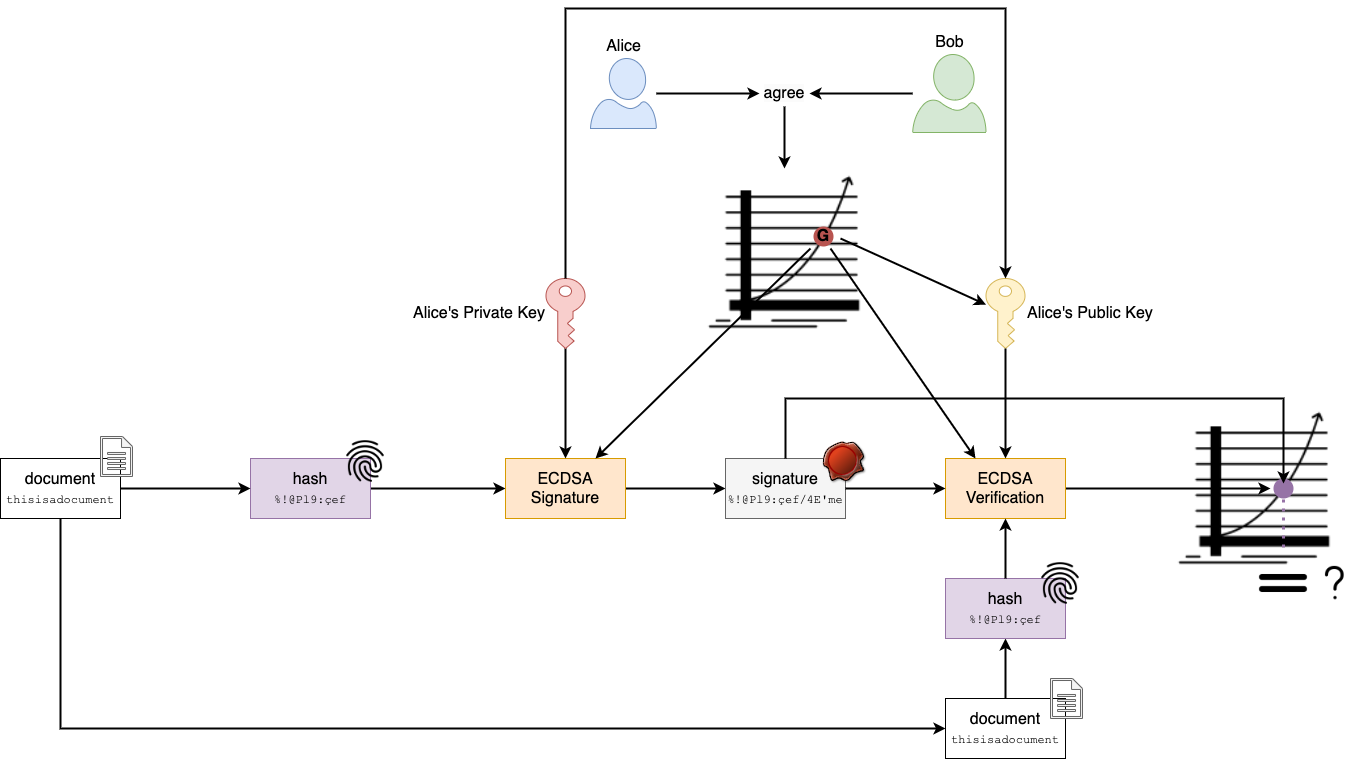
Processus de signature et vérification ECDSA

Si on résume, la signature d’un document envoyé comprend l’abscisse d’un point calculé par multiplication par un nombre aléatoire d’un point de base connu du signataire et récepteur sur une courbe elliptique ainsi qu’une valeur calculée à partir de l’abscisse de ce point, l’empreinte du document et la clé privée du signataire. La vérification de cette signature consiste à calculer un point à partir du point de base sur la courbe, de l’empreinte recalculée du document reçu, des valeurs de la signature reçue ainsi que de la clé publique du signataire. Si l’abscisse de ce point calculé correspond à la valeur d’abscisse transmise dans la signature, la signature est correcte.

Clairement, l’algorithme ECDSA est plus complexe que RSA, qui consiste à réaliser l’opération suivante :

  • Alice génère une signature $y = x^d\bmod{n}$, où $x$ est l’empreinte du document à signer alors que $d$ et $n$ composent la clé privée d’Alice.
  • Bob vérifie la signature en calculant d’abord $x = y^e\bmod{n}$, où $y$ est la signature reçue alors que $e$ et $n$ composent la clé publique d’Alice. Puis il compare $x$ avec l’empreinte du message reçu.

Quel est alors l’avantage d’ECDSA par rapport à RSA ?
L’utilisation de courbes elliptiques permet en fait de manipuler des clés plus courtes. Avec RSA, on considère de manière générale qu’il faut une clé d’au moins 2048 bits pour garantir un niveau de sécurité satisfaisant. Avec ECDSA, une courbe elliptique sur 256 bits est considérée satisfaisante. La génération de signatures avec ECDSA est donc plus rapide mais aussi la longueur des signatures ECDSA est plus courte (au moins 4 fois plus courte). La durée de la vérification reste équivalente ou légèrement plus rapide avec RSA du fait de la simplicité de l’opération engagée via RSA.

Afin d’illustrer tout ça, j’ai intégré et testé le calcul de vitesse d’exécution des signatures RSA, ECDSA et EdDSA dans mon outil cryptauditor qui permet de mesurer la vitesse d’exécution d’algorithmes de cryptographie. Les mesures ont été effectuées sur un MacBook Pro avec processeur Intel Core i5 2,4 GHz Quad-Core avec 16 Go de mémoire et tournant sur macOS Ventura (version 13.3.1). En utilisant une clé RSA de 3072 bits et des courbes elliptiques ECDSA et EdDSA de 256 bits, voici le résultat :

$ python3 cryptauditor.py -s SIGN-ALL -k 3072 -r 10000
Performing 10000 rounds of RSA-PSS signature and verification with a 3072-bit random key on 1KB of random data hashed with SHA-256
Performing 10000 rounds of ECDSA signature and verification with a 256-bit (P-256) elliptic curve on 1KB of random data hashed with SHA-256
Performing 10000 rounds of EdDSA signature and verification with a 256-bit (Ed25519) elliptic curve on 1KB of random data hashed with SHA-512
Signature speed ranking:
1 - EdDSA - 0.693ms (+0.0ms)
2 - ECDSA - 0.785ms (+0.092ms)
3 - RSA-PSS - 4.188ms (+3.495ms)
Verification speed ranking:
1 - RSA-PSS - 0.732ms (+0.0ms)
2 - ECDSA - 1.552ms (+0.82ms)
3 - EdDSA - 2.128ms (+1.396ms)

La pratique a confirmé la théorie !

Chiffrement ECIES

Il existe quelques algorithmes de chiffrement adaptés sur courbes elliptiques. L’algorithme de chiffrement sur courbes elliptiques le plus célèbre est probablement l’Elliptic Curve Integrated Encryption Scheme (ECIES) qui est qualifié d’hybride car combinant cryptographie asymétrique et symétrique. Pour qu’Alice chiffre un message $M$ pour Bob :

  • Alice et Bob se mettent d’accord sur une courbe et un point de base $G$, une fonction de dérivation de clé ou Key Derivation Function (KDF) et un algorithme de chiffrement authentifié (comme AES-GCM).
  • Bob génère une paire de clés publique-privée où un nombre aléatoire secret $k$ est la clé privée et $P = kG$ est la clé publique correspondante.
  • Alice partage sa clé publique $P$ à Bob.
  • Alice choisit un nombre aléatoire $r$ et calcule le point $Q = rG$ qui est une clé éphémère ou ephemeral key (valable pour une seule utilisation).
  • Alice calcule un secret partagé ECDH $S = rP$.
  • Bob dérive une clé $K$ à partir de $S$ à l’aide de la KDF.
  • Bob chiffre le message $M$ avec la clé $K$ et l’algorithme de chiffrement authentifié puis transmet le chiffré ou ciphertext $C$, le tag $T$ et $Q$ à Alice.

Pour qu’Alice déchiffre le chiffré $C$ et vérifie le tag $T$ reçu :

  • Bob calcule un secret partagé ECDH $S = kQ$. Ici $kQ = krG = rP$ qui est bien le même secret calculé par Alice de son côté.
  • Alice dérive la clé $K$ à partir de $S$ à l’aide de la KDF.
  • Alice vérifie le tag $T$ et déchiffre le chiffré $C$ à l’aide de $K$ et de l’algorithme de chiffrement authentifié pour retrouver le message $M$. On voit bien qu’ECIES utilise du chiffrement symétrique (utilisation d’une clé partagée K) déterminée grâce à la cryptographie asymétrique (utilisation d’ECDH).

Le chiffrement des données avec courbes elliptiques est moins commun que l’échange de clés ou les signatures du fait de limitations sur la taille des données pouvant être chiffrées.

Conclusion

Nous avons découvert ensemble dans cet article ce que sont les courbes elliptiques et comment elles sont utiles en cryptographie pour l’échange de clés, la signature numérique ou le chiffrement. Elles aujourd’hui largement utilisées dans de nombreux protocoles réseau ou logiciels car offrent un très bon niveau de sécurité et des performances très intéressantes.

Sources

Traductions